UInt/SInt
Description
The UInt/SInt type corresponds to a vector of bits that can be used for signed/unsigned integer arithmetic.
Declaration
The syntax to declare an integer is as follows: (everything between [] is optional)
Syntax |
Description |
Return |
|---|---|---|
UInt[()]
SInt[()]
|
Create an unsigned/signed integer, bits count is inferred |
UInt
SInt
|
UInt(x bits)
SInt(x bits)
|
Create an unsigned/signed integer with x bits |
UInt
SInt
|
U(value: Int[,x bits])
U(value: BigInt[,x bits])
S(value: Int[,x bits])
S(value: BigInt[,x bits])
|
Create an unsigned/signed integer assigned with ‘value’ |
UInt
SInt
|
U”[[size’]base]value”
S”[[size’]base]value”
|
Create an unsigned/signed integer assigned with ‘value’ (Base : ‘h’, ‘d’, ‘o’, ‘b’) |
UInt
SInt
|
Create an unsigned integer assigned with the value specified by elements |
UInt
SInt
|
val myUInt = UInt(8 bits)
myUInt := U(2,8 bits)
myUInt := U(2)
myUInt := U"0000_0101" // Base per default is binary => 5
myUInt := U"h1A" // Base could be x (base 16)
// h (base 16)
// d (base 10)
// o (base 8)
// b (base 2)
myUInt := U"8'h1A"
myUInt := 2 // You can use a Scala Int as a literal value
val myBool := myUInt === U(7 -> true,(6 downto 0) -> false)
val myBool := myUInt === U(myUInt.range -> true)
// For assignment purposes, you can omit the U/S, which also allows the use of the [default -> ???] feature
myUInt := (default -> true) // Assign myUInt with "11111111"
myUInt := (myUInt.range -> true) // Assign myUInt with "11111111"
myUInt := (7 -> true, default -> false) // Assign myUInt with "10000000"
myUInt := ((4 downto 1) -> true, default -> false) // Assign myUInt with "00011110"
Operators
The following operators are available for the UInt and SInt types:
Logic
Operator |
Description |
Return type |
|---|---|---|
x ^ y |
Logical XOR |
Bool |
~x |
Bitwise NOT |
T(w(x) bits) |
x & y |
Bitwise AND |
T(max(w(x), w(y)) bits) |
x | y |
Bitwise OR |
T(max(w(x), w(y)) bits) |
x ^ y |
Bitwise XOR |
T(max(w(x), w(y)) bits) |
x.xorR |
XOR all bits of x |
Bool |
x.orR |
OR all bits of x |
Bool |
x.andR |
AND all bits of x |
Bool |
x >> y |
Arithmetic shift right, y : Int |
T(w(x) - y bits) |
x >> y |
Arithmetic shift right, y : UInt |
T(w(x) bits) |
x << y |
Arithmetic shift left, y : Int |
T(w(x) + y bits) |
x << y |
Arithmetic shift left, y : UInt |
T(w(x) + max(y) bits) |
x |>> y |
Logical shift right, y : Int/UInt |
T(w(x) bits) |
x |<< y |
Logical shift left, y : Int/UInt |
T(w(x) bits) |
x.rotateLeft(y) |
Logical left rotation, y : UInt/Int |
T(w(x) bits) |
x.rotateRight(y) |
Logical right rotation, y : UInt/Int |
T(w(x) bits) |
x.clearAll[()] |
Clear all bits |
|
x.setAll[()] |
Set all bits |
|
x.setAllTo(value : Boolean) |
Set all bits to the given Boolean value |
|
x.setAllTo(value : Bool) |
Set all bits to the given Bool value |
Note
x rotateLeft y and x rotateRight y are also valid syntax.
Note
Notice the difference between x >> 2:T(w(x)-2) and x >> U(2):T(w(x)).
The difference is that in the first case 2 is an Int (which can be seen as an
“elaboration integer”), and in the second case it is a hardware signal.
val a, b, c = SInt(32 bits)
a := S(5)
b := S(10)
// Bitwise operators
c := ~(a & b) // Inverse(a AND b)
assert(c.getWidth == 32)
// Shift
val arithShift = UInt(8 bits) << 2 // shift left (resulting in 10 bits)
val logicShift = UInt(8 bits) |<< 2 // shift left (resulting in 8 bits)
assert(arithShift.getWidth == 10)
assert(logicShift.getWidth == 8)
// Rotation
val rotated = UInt(8 bits) rotateLeft 3 // left bit rotation
assert(rotated.getWidth == 8)
// Set all bits of b to True when all bits of a are True
when(a.andR) { b.setAll() }
Arithmetic
Operator |
Description |
Return |
|---|---|---|
x + y |
Addition |
T(max(w(x), w(y)) bits) |
x +^ y |
Addition with carry |
T(max(w(x), w(y)) + 1 bits) |
x +| y |
Addition by sat carry bit |
T(max(w(x), w(y)) bits) |
x - y |
Subtraction |
T(max(w(x), w(y)) bits) |
x -^ y |
Subtraction with carry |
T(max(w(x), w(y)) + 1 bits) |
x -| y |
Subtraction by sat carry bit |
T(max(w(x), w(y)) bits) |
x * y |
Multiplication |
T(w(x) + w(y)) bits) |
x / y |
Division |
T(w(x) bits) |
x % y |
Modulo |
T(min(w(x), w(y)) bits) |
val a, b, c = UInt(8 bits)
a := U"xf0"
b := U"x0f"
c := a + b
assert(c === U"8'xff")
val d = a +^ b
assert(d === U"9'x0ff")
val e = a +| U"8'x20"
assert(e === U"8'xff")
Note
Notice how simulation assertions are made here (with ===), as opposed to elaboration
assertions in the previous example (with ==).
Comparison
Operator |
Description |
Return type |
|---|---|---|
x === y |
Equality |
Bool |
x =/= y |
Inequality |
Bool |
x > y |
Greater than |
Bool |
x >= y |
Greater than or equal |
Bool |
x < y |
Less than |
Bool |
x <= y |
Less than or equal |
Bool |
val a = U(5, 8 bits)
val b = U(10, 8 bits)
val c = UInt(2 bits)
when (a > b) {
c := U"10"
} elsewhen (a =/= b) {
c := U"01"
} elsewhen (a === U(0)) {
c.setAll()
} otherwise {
c.clearAll()
}
Type cast
Operator |
Description |
Return |
|---|---|---|
x.asBits |
Binary cast to Bits |
Bits(w(x) bits) |
x.asUInt |
Binary cast to UInt |
UInt(w(x) bits) |
x.asSInt |
Binary cast to SInt |
SInt(w(x) bits) |
x.asBools |
Cast into a array of Bool |
Vec(Bool, w(x)) |
S(x: T) |
Cast a Data into a SInt |
SInt(w(x) bits) |
U(x: T) |
Cast a Data into an UInt |
UInt(w(x) bits) |
x.intoSInt |
Convert to SInt expanding sign bit |
SInt(w(x) + 1 bits) |
To cast a Bool, a Bits, or an SInt into a UInt, you can use U(something). To cast things into an SInt, you can use S(something).
// Cast an SInt to Bits
val myBits = mySInt.asBits
// Create a Vector of Bool
val myVec = myUInt.asBools
// Cast a Bits to SInt
val mySInt = S(myBits)
Bit extraction
Operator |
Description |
Return |
|---|---|---|
x(y) |
Readbit, y : Int/UInt |
Bool |
x(offset, width) |
Read bitfield, offset: UInt, width: Int |
T(width bits) |
x(range) |
Read a range of bits. Ex : myBits(4 downto 2) |
T(range bits) |
x(y) := z |
Assign bits, y : Int/UInt |
Bool |
x(offset, width) := z |
Assign bitfield, offset: UInt, width: Int |
T(width bits) |
x(range) := z |
Assign a range of bit. Ex : myBits(4 downto 2) := U”010” |
T(range bits) |
// get the bit at index 4
val myBool = myUInt(4)
// assign bit 1 to True
mySInt(1) := True
// Range
val myUInt_8bits = myUInt_16bits(7 downto 0)
val myUInt_7bits = myUInt_16bits(0 to 6)
val myUInt_6bits = myUInt_16Bits(0 until 6)
mySInt_8bits(3 downto 0) := mySInt_4bits
Misc
Operator |
Description |
Return |
|---|---|---|
x.getWidth |
Return bitcount |
Int |
x.msb |
Return the most significant bit |
Bool |
x.lsb |
Return the least significant bit |
Bool |
x.range |
Return the range (x.high downto 0) |
Range |
x.high |
Return the upper bound of the type x |
Int |
x ## y |
Concatenate, x->high, y->low |
Bits(w(x) + w(y) bits) |
x @@ y |
Concatenate x:T with y:Bool/SInt/UInt |
T(w(x) + w(y) bits) |
x.subdivideIn(y slices) |
Subdivide x into y slices, y: Int |
Vec(T, y) |
x.subdivideIn(y bits) |
Subdivide x into multiple slices of y bits, y: Int |
Vec(T, w(x)/y) |
x.resize(y) |
Return a resized copy of x, if enlarged, it is filled with zero
for UInt or filled with the sign for SInt, y: Int
|
T(y bits) |
x.resized |
Return a version of x which is allowed to be automatically
resized where needed
|
T(w(x) bits) |
myUInt.twoComplement(en: Bool) |
Use the two’s complement to transform an UInt into an SInt |
SInt(w(myUInt) + 1, bits) |
mySInt.abs |
Return the absolute value as a UInt value |
UInt(w(mySInt), bits) |
mySInt.abs(en: Bool) |
Return the absolute value as a UInt value when en is True |
UInt(w(mySInt), bits) |
mySInt.sign |
Return most significant bit |
Bool |
x.expand |
Return x with 1 bit expand |
T(w(x)+1 bits) |
mySInt.absWithSym |
Return the absolute value of the UInt value with symmetric, shrink 1 bit |
UInt(w(mySInt) - 1 bits) |
myBool := mySInt.lsb // equivalent to mySInt(0)
// Concatenation
val mySInt = mySInt_1 @@ mySInt_1 @@ myBool
val myBits = mySInt_1 ## mySInt_1 ## myBool
// Subdivide
val sel = UInt(2 bits)
val mySIntWord = mySInt_128bits.subdivideIn(32 bits)(sel)
// sel = 0 => mySIntWord = mySInt_128bits(127 downto 96)
// sel = 1 => mySIntWord = mySInt_128bits( 95 downto 64)
// sel = 2 => mySIntWord = mySInt_128bits( 63 downto 32)
// sel = 3 => mySIntWord = mySInt_128bits( 31 downto 0)
// If you want to access in reverse order you can do:
val myVector = mySInt_128bits.subdivideIn(32 bits).reverse
val mySIntWord = myVector(sel)
// Resize
myUInt_32bits := U"32'x112233344"
myUInt_8bits := myUInt_32bits.resized // automatic resize (myUInt_8bits = 0x44)
myUInt_8bits := myUInt_32bits.resize(8) // resize to 8 bits (myUInt_8bits = 0x44)
// Two's complement
mySInt := myUInt.twoComplement(myBool)
// Absolute value
mySInt_abs := mySInt.abs
FixPoint operations
For fixpoint, we can divide it into two parts:
Lower bit operations (rounding methods)
High bit operations (saturation operations)
Lower bit operations
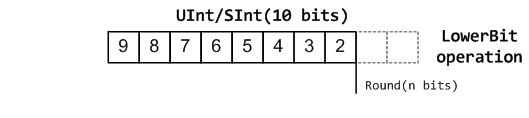
About Rounding: https://en.wikipedia.org/wiki/Rounding
SpinalHDL-Name |
Wikipedia-Name |
API |
Mathematic Algorithm |
return(align=false) |
Supported |
|---|---|---|---|---|---|
FLOOR |
RoundDown |
floor |
floor(x) |
w(x)-n bits |
Yes |
FLOORTOZERO |
RoundToZero |
floorToZero |
sign*floor(abs(x)) |
w(x)-n bits |
Yes |
CEIL |
RoundUp |
ceil |
ceil(x) |
w(x)-n+1 bits |
Yes |
CEILTOINF |
RoundToInf |
ceilToInf |
sign*ceil(abs(x)) |
w(x)-n+1 bits |
Yes |
ROUNDUP |
RoundHalfUp |
roundUp |
floor(x+0.5) |
w(x)-n+1 bits |
Yes |
ROUNDDOWN |
RoundHalfDown |
roundDown |
ceil(x-0.5) |
w(x)-n+1 bits |
Yes |
ROUNDTOZERO |
RoundHalfToZero |
roundToZero |
sign*ceil(abs(x)-0.5) |
w(x)-n+1 bits |
Yes |
ROUNDTOINF |
RoundHalfToInf |
roundToInf |
sign*floor(abs(x)+0.5) |
w(x)-n+1 bits |
Yes |
ROUNDTOEVEN |
RoundHalfToEven |
roundToEven |
No |
||
ROUNDTOODD |
RoundHalfToOdd |
roundToOdd |
No |
Note
The RoundToEven and RoundToOdd modes are very special, and are used in some big data statistical fields with high accuracy concerns, SpinalHDL doesn’t support them yet.
You will find ROUNDUP, ROUNDDOWN, ROUNDTOZERO, ROUNDTOINF, ROUNDTOEVEN, ROUNTOODD are very close in behavior, ROUNDTOINF is the most common. The behavior of rounding in different programming languages may be different.
Programming language |
default-RoundType |
Example |
comments |
|---|---|---|---|
Matlab |
ROUNDTOINF |
round(1.5)=2,round(2.5)=3;round(-1.5)=-2,round(-2.5)=-3 |
round to ±Infinity |
python2 |
ROUNDTOINF |
round(1.5)=2,round(2.5)=3;round(-1.5)=-2,round(-2.5)=-3 |
round to ±Infinity |
python3 |
ROUNDTOEVEN |
round(1.5)=round(2.5)=2; round(-1.5)=round(-2.5)=-2 |
close to Even |
Scala.math |
ROUNDTOUP |
round(1.5)=2,round(2.5)=3;round(-1.5)=-1,round(-2.5)=-2 |
always to +Infinity |
SpinalHDL |
ROUNDTOINF |
round(1.5)=2,round(2.5)=3;round(-1.5)=-2,round(-2.5)=-3 |
round to ±Infinity |
Note
In SpinalHDL ROUNDTOINF is the default RoundType (round = roundToInf)
val A = SInt(16 bits)
val B = A.roundToInf(6 bits) // default 'align = false' with carry, got 11 bit
val B = A.roundToInf(6 bits, align = true) // sat 1 carry bit, got 10 bit
val B = A.floor(6 bits) // return 10 bit
val B = A.floorToZero(6 bits) // return 10 bit
val B = A.ceil(6 bits) // ceil with carry so return 11 bit
val B = A.ceil(6 bits, align = true) // ceil with carry then sat 1 bit return 10 bit
val B = A.ceilToInf(6 bits)
val B = A.roundUp(6 bits)
val B = A.roundDown(6 bits)
val B = A.roundToInf(6 bits)
val B = A.roundToZero(6 bits)
val B = A.round(6 bits) // SpinalHDL uses roundToInf as the default rounding mode
val B0 = A.roundToInf(6 bits, align = true) // ---+
// |--> equal
val B1 = A.roundToInf(6 bits, align = false).sat(1) // ---+
Note
Only floor and floorToZero work without the align option; they do not need a carry bit. Other rounding operations default to using a carry bit.
round Api
API |
UInt/SInt |
description |
Return(align=false) |
Return(align=true) |
|---|---|---|---|---|
floor |
Both |
w(x)-n bits |
w(x)-n bits |
|
floorToZero |
SInt |
equal to floor in UInt |
w(x)-n bits |
w(x)-n bits |
ceil |
Both |
w(x)-n+1 bits |
w(x)-n bits |
|
ceilToInf |
SInt |
equal to ceil in UInt |
w(x)-n+1 bits |
w(x)-n bits |
roundUp |
Both |
simple for HW |
w(x)-n+1 bits |
w(x)-n bits |
roundDown |
Both |
w(x)-n+1 bits |
w(x)-n bits |
|
roundToInf |
SInt |
most Common |
w(x)-n+1 bits |
w(x)-n bits |
roundToZero |
SInt |
equal to roundDown in UInt |
w(x)-n+1 bits |
w(x)-n bits |
round |
Both |
SpinalHDL chose roundToInf |
w(x)-n+1 bits |
w(x)-n bits |
Note
Although roundToInf is very common, roundUp has the least cost and good timing, with almost no performance loss.
As a result, roundUp is strongly recommended for production use.
High bit operations
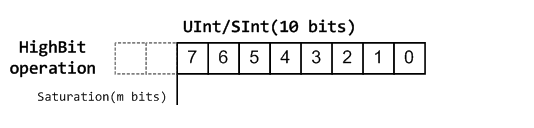
function |
Operation |
Positive-Op |
Negative-Op |
|---|---|---|---|
sat |
Saturation |
when(Top[w-1, w-n].orR) set maxValue |
When(Top[w-1, w-n].andR) set minValue |
trim |
Discard |
N/A |
N/A |
symmetry |
Symmetric |
N/A |
minValue = -maxValue |
Symmetric is only valid for SInt.
val A = SInt(8 bits)
val B = A.sat(3 bits) // return 5 bits with saturated highest 3 bits
val B = A.sat(3) // equal to sat(3 bits)
val B = A.trim(3 bits) // return 5 bits with the highest 3 bits discarded
val B = A.trim(3 bits) // return 5 bits with the highest 3 bits discarded
val C = A.symmetry // return 8 bits and symmetry as (-128~127 to -127~127)
val C = A.sat(3).symmetry // return 5 bits and symmetry as (-16~15 to -15~15)
fixTo function
Two ways are provided in UInt/SInt to do fixpoint:
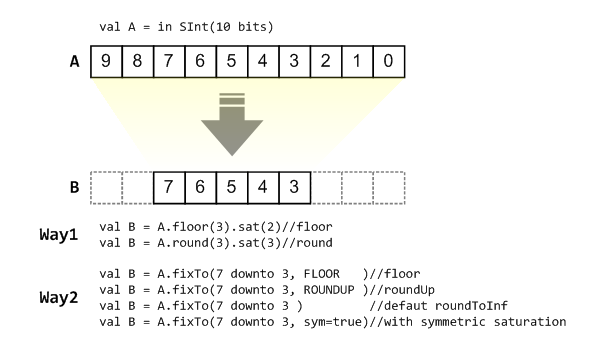
fixTo is strongly recommended in your RTL work, you don’t need to handle carry bit alignment and bit width calculations manually like Way1 in the above diagram.
Factory Fix function with Auto Saturation:
Function |
Description |
Return |
|---|---|---|
fixTo(section, roundType, symmetric) |
Factory FixFunction |
section.size bits |
val A = SInt(16 bits)
val B = A.fixTo(10 downto 3) // default RoundType.ROUNDTOINF, sym = false
val B = A.fixTo( 8 downto 0, RoundType.ROUNDUP)
val B = A.fixTo( 9 downto 3, RoundType.CEIL, sym = false)
val B = A.fixTo(16 downto 1, RoundType.ROUNDTOINF, sym = true )
val B = A.fixTo(10 downto 3, RoundType.FLOOR) // floor 3 bit, sat 5 bit @ highest
val B = A.fixTo(20 downto 3, RoundType.FLOOR) // floor 3 bit, expand 2 bit @ highest